Running a PCA-ANOVA in R is fairly straightforward. In this post we’ll focus on doing a temporal PCA on clusters of ERP channels. First you will want to arrange the data in one file. If you are coming from Net Station, you can export your ERP averaged files to text and then use MCAT to create averaged channels to input into the PCA. MCAT does three things that are useful in this case: 1) MCAT creates average channels; 2) MCAT rotates the channels so that the columns represent time, instead of the EGI default method of columns representing different channels; 3) MCAT will concatenate all of the subjects together.
By default, MCAT creates 10 channels from a 128 channel EGI Net. It is simple to modify the number and composition of each channel, but for the purposes of this walkthrough, we will use the defaults. The default are 5 channels per hemisphere, representing Frontal, Central, Temporal, Parietal, and Occipital regions. In this example, we have 24 subjects and they see two conditions: congruent and incongruent.
In order to run a PCA with rotation in R, we will need the psych package:
install.packages('psych', depend=T)
Next we want to read the data into R
thedata = read.table("demo_500.txt", sep='\t', header=F, skip=0)
This will read the text file into R, noticing that it is tab-delimited and has no “header” which would be a listing of variables. If you used MCAT, you are likely going to use this line as is. The next step is running the PCA in R. To do so, we use the following command:
my.pca = principal(thedata[seq(26,150,2)], nfactors=5, rotate='varimax', scores=TRUE, covar=F)
Stepping through this command, this will run a PCA on time points 26-150, skipping every other time point. I chose these values because my ERP included 100 millisecond baseline, recorded at 250Hz, breaks down to 4 milliseconds per sample, 25*4=100. We don’t want to include the baseline in the PCA for this example. I skip every other sample because of the high temporal correlation in the data and skipping every other value will give you plenty of resolution to detect the “slow” ERP components. You should feel free to try it both ways. Next, we are going to start with 5 components and use a varimax rotation, which will force the components to be orthogonal. Finally, this is running the PCA using a correlation matrix, the alternative is to use a covariance matrix. The result is that a correlation matrix will add a bit of normalization to your PCA.
Truthfully, I had some difficulty getting the covariance matrix PCA to give me the same values as other software packages (e.g. SAS). The Correlation Matrix results were almost identical to SAS. I’ll debug this later.
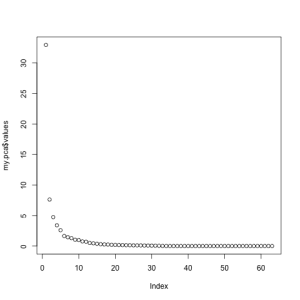
At this point, we need to see if 5 components correctly captures the variance of the original data. To do this, most people use the Scree plot, originally developed by Cattell. The general idea is to retain the factors until you reach the point where the rocks would collect at the base of a mountain. Alternative solutions to choosing the number of factors are 1) retain values until you reach an Eigan Value of 1.0; 2) retain values until you account for a pre-determined percent of the variance. Both of these methods will unfortunately leave you with factors that account for very little variance. The validity of using these low-variance components for later analyses is arguable, though I tend to avoid using them. You can see in the scree chart below that we would choose between 5 and 6 components. For the sake of ease, today I will choose 5.
At this point, the PCA has created 5 factors that represent each CHANNEL (or averaged channel) for each condition, for each subject. Going into the PCA you had 2 conditions, 10 channels, and 24 subjects, which was represented as 480 rows in the input file. Now for each of those 480 rows, you have 5 values, representing the data reduced time course of each channel within condition within subject. The next step is to rename these factors to represent the appropriate channel and conditions as well as organize them into one row for each participant so that you can do repeated-measures ANOVAs on the data.
The following code rotates the matrix, to make renaming easier. Then we cast the data frame as a matrix and re-specify it to be 24 rows (the number of subjects). Then we send it back to a data frame and add “labels” to the data frame representing each channel, condition, and factor. Channels are here labeled as the first two letters, so FL would be “front left” and so on.
rotdata = t(my.pca$scores) #rotates the data.frame
rename = matrix(rotdata, nrow=24, byrow=TRUE) #nrow = #subjects
rename = data.frame(rename); #convert it back to a dataframe
labels = c("FLcon1 FLcon2 FLcon3 FLcon4 FLcon5 FRcon1 FRcon2 FRcon3 FRcon4 FRcon5 CLcon1 CLcon2 CLcon3 CLcon4 CLcon5 CRcon1 CRcon2 CRcon3 CRcon4 CRcon5 PLcon1 PLcon2 PLcon3 PLcon4 PLcon5 PRcon1 PRcon2 PRcon3 PRcon4 PRcon5 OLcon1 OLcon2 OLcon3 OLcon4 OLcon5 ORcon1 ORcon2 ORcon3 ORcon4 ORcon5 TLcon1 TLcon2 TLcon3 TLcon4 TLcon5 TRcon1 TRcon2 TRcon3 TRcon4 TRcon5 FLinc1 FLinc2 FLinc3 FLinc4 FLinc5 FRinc1 FRinc2 FRinc3 FRinc4 FRinc5 CLinc1 CLinc2 CLinc3 CLinc4 CLinc5 CRinc1 CRinc2 CRinc3 CRinc4 CRinc5 PLinc1 PLinc2 PLinc3 PLinc4 PLinc5 PRinc1 PRinc2 PRinc3 PRinc4 PRinc5 OLinc1 OLinc2 OLinc3 OLinc4 OLinc5 ORinc1 ORinc2 ORinc3 ORinc4 ORinc5 TLinc1 TLinc2 TLinc3 TLinc4 TLinc5 TRinc1 TRinc2 TRinc3 TRinc4 TRinc5"); #assign variable names
names(rename) = unlist(strsplit(labels, split=" ")); #put names into dataframe
I make these labels in the SPSS Label Maker and so I have R split the continuous string of values into separate values. At this point you have a data frame “rename” that has 24 rows and 100 variables (10 electrodes * 2 conditions * 5 factors = 100 variables). At this point you are ready to run an ANOVA on each of the five components that were extracted. I like how easy this is to do in the “ez” package, so we’ll outline those steps:
factor1 = names(rename[seq(1,100,5)]) f1 = rename[factor1] f1$subject = seq(1,24)
These three lines breakout the first factor into a second dataset. We then use melt() to convert the data from wide format to long format. Next we need to add some descriptors to the data, these are variables in long format that serve to describe characteristics of that particular data point. I use rep to do this and exploit the organized format of the data. Using the code below, I add variables region, hemisphere, and condition. You could also do this with a series of functions of if/then or ifelse() commands.
longdata = melt(f1, id.vars=c("subject") )
longdata$region = rep(c('F', 'C', 'P', 'O', 'T'), each=48) #2 hemispheres, 5 regions, 24 subjects
longdata$hemisphere = rep(c('L', 'R'), each=24)
longdata$condition = rep(c('con', 'inc'), each=240)
Finally we are ready to actually run the ANOVA on this first factor with a condition X hemisphere X region repeated-measures design.
library(ez)
ezANOVA(longdata, dv='value', wid=subject, within=.('condition', 'hemisphere', 'region'), type=)
The results are nicely printed out, a subset is shown below. We have identified a main effect for hemisphere as well as region, these are qualified by a hemisphere X region interaction.
$ANOVA Effect DFn DFd F p p<.05 2 condition 1 23 0.06986913 7.938816e-01 3 hemisphere 1 23 7.88955879 9.965560e-03 * 4 region 4 92 9.88646606 1.066086e-06 * 5 condition:hemisphere 1 23 0.11050484 7.425808e-01 6 condition:region 4 92 1.04554033 3.881822e-01 7 hemisphere:region 4 92 3.91039384 5.607436e-03 * 8 condition:hemisphere:region 4 92 1.24818805 2.962026e-01
Now that you’ve identified main effects or interactions in this first factor, you can repeat the process for the other factors. Finally you can see where the factors were most active by looking at the “factor loadings” These are exposed in R and the Psych toolbox as by running:
my.pca$loadings
Most people seem to agree that a loading of 0.4 or higher (absolute value) are worth reporting. Next EEG post, I’ll show how to do the same analyses using the ERP PCA Toolkit that was talked about before.